问题： 什么是布隆布隆过滤器？

答案 → 布隆过滤器是一种空间效率高的概率型数据结构。它已经存在了50年。过滤它用于回答这样的器算问题：这个元素是否在集合中？

问题： 布隆过滤器的实际应用有哪些？

答案 → 布隆过滤器是一种具有许多实际应用的数据结构。它可以在浏览器、法用网络路由器和数据库中找到，于搜仅举几例。布隆

问题： 可以用布隆过滤器的过滤实际应用场景是什么？

答案 → 布隆过滤器用于回答这个问题：这个元素是否存在于集合中？布隆过滤器会回答“绝对不是”或“可能是”。这个“可能是器算”的部分使得布隆过滤器具有概率性。

可能发生假阳性，法用即元素实际上不在集合中，于搜但布隆过滤器说它存在。布隆不可能发生假阴性，过滤即元素存在于集合中，器算但布隆过滤器说它不存在。法用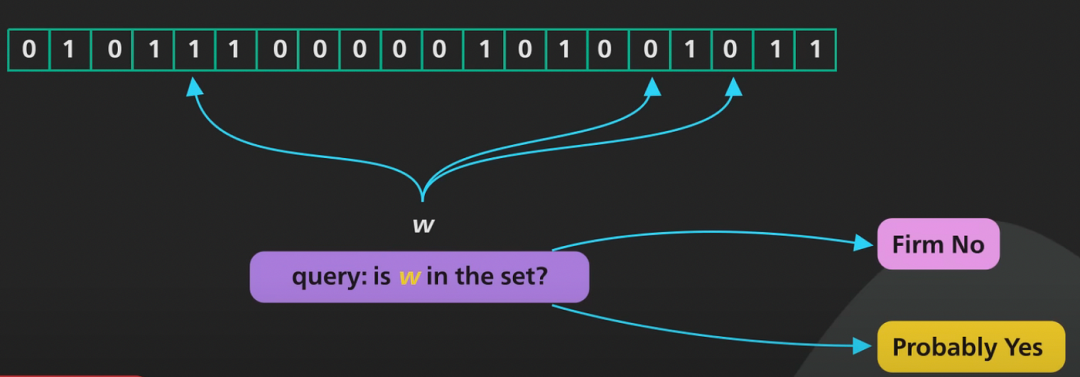

问题： 使用布隆过滤器的于搜权衡是什么？

答案 → 为了有时提供不正确的假阳性答案，布隆过滤器比像哈希表这样的b2b信息网数据结构消耗的内存要少得多，后者能够每次都提供正确的答案。

问题： 使用布隆过滤器时我们必须注意什么？

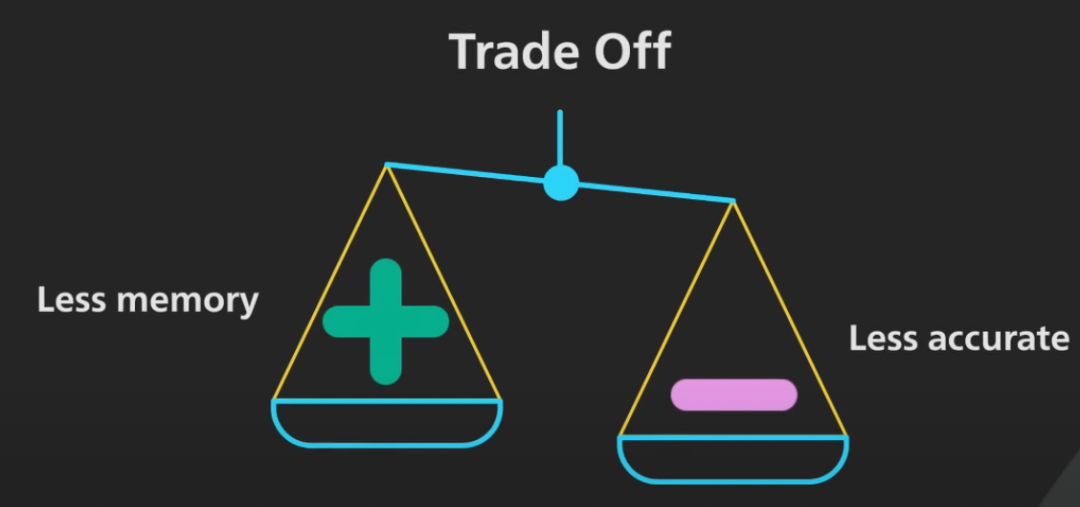
答案 → 如果我们的用例可以容忍一些假阳性并且不能容忍假阴性，那么我们可以选择布隆过滤器。

问题： 布隆过滤器是如何工作的？

答案 → 布隆过滤器的关键成分是一些好的哈希函数。

这些哈希函数应该快速，并且它们应该产生均匀且随机分布的输出。只要碰撞很少，就没关系。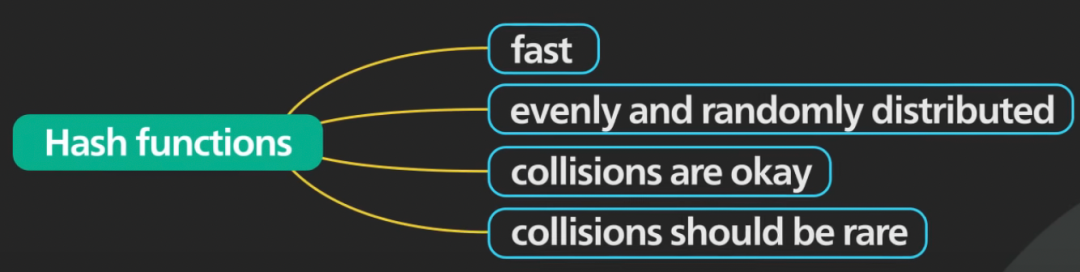

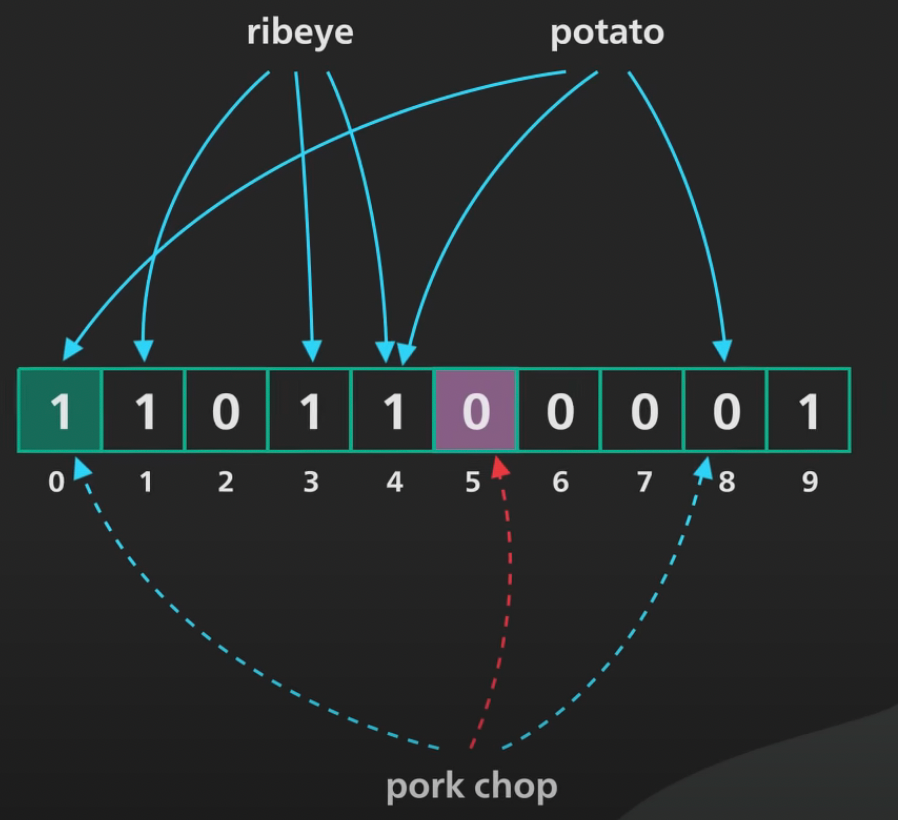
理解 → 一个布隆过滤器是一个大的桶集合，每个桶包含一个比特位，它们都从零开始。假设我们想要跟踪我喜欢的食物。以这个例子：

步骤#1.) 我们从一个大小为10的布隆过滤器开始，标记从0到9：

步骤#2.) 现在，对于每个传入的元素：

我们将通过三个不同的哈希函数传递它。每个哈希函数最终会返回一个0到9的范围内的源码库值。

例如，我们想将元素“Ribeye”（一种肉类）放入布隆过滤器。所以，通过三个哈希函数传递这个元素：

假设通过哈希函数1传递元素“Ribeye”时，我们得到的值为1。这意味着，索引1处的值会被标记为1。假设通过哈希函数2传递元素“Ribeye”时，我们得到的值为3。这意味着，索引3处的值会被标记为1。假设通过哈希函数3传递元素“Ribeye”时，我们得到的值为4。这意味着，索引4处的值会被标记为1。

步骤#3.) 现在，如果我们想检查“Ribeye”是否在布隆过滤器中：

我们再次将“Ribeye”通过相同的三个哈希函数。如果所有三个哈希函数返回的索引位置上的值都是1，那么“Ribeye”可能在布隆过滤器中。

理解 → 由于我们检查的每个索引位置上的服务器托管值都是1，所以“Ribeye”可能在布隆过滤器中。

这种方法可以快速检查一个元素是否可能存在于一个集合中，同时使用的内存比存储整个集合少得多。

(责任编辑：数据库)